Airfoils-Part 1
By Chris Heintz (originally published EAA Light Plane World, May 1987)
Analysis is necessary; but only a synthetic view will give us the whole picture. It is a bit like somebody trying to understand the human body by studying the skeleton only, or the chemicals of the body only, etc.: the failure of modern medicine comes from this fact. Scientists look at the parts of a corpse and decide they know something about a living body!
But, let us go back to something less serious (!?!) and look at the airfoil or wing section of our airplane in such a way that we will have a little better understanding of how our aircraft flies.
Relative Motion
Today it is universally accepted that an airfoil in motion through still air and air blowing over a stationary airfoil have the same effects. This was not the case in scientific circles some 120 years ago, but now is common knowledge, and justifies the wind tunnel tests where true air flows over an airfoil and from which we can predict characteristics of an airplane moving through still air. The important thing is the relative speed of airfoil and air.
Reynolds Numbers
Early investigations into the theory of fluid dynamics have predicted a certain number of constants to which similar disturbances (and an airfoil in the air is a disturbance) produce similar effects - in hydrodynamics, these are referred to as 'Froude Numbers" (hulls of boats); in high speed aerodynamics the "Mach Number' are other examples. For our smaller and slower aircraft, the only "number" which really needs to be considered is the "Reynolds Number" and it is defined as:
Re = V x I / v
Where:
V = Relative speed (m/sec)
I = typical "length" of a solid body (M)
v = kinematic viscosity of the air (sec/m2)
Re is a dimensionless number, which makes it independent of the measuring systems. The cinematic viscosity is to a certain extent dependent on the density of the air, but for our aircraft flying below 12,000 ft., it can be assumed constant (equivalent to 15 x 106 sec/m2 in metric).
The speed can easily be converted to metric:
1 mph = 1.15 Kts. = 1.61 km/h = 1.61 / 3.6 m/s = .45 m/sec.
The same applies to the length:
1 ft. = .305 m.
Our small aircraft have a wing chord, which is the "length" to use when talking about airfoils, of some 5 ft. equivalent to 1.5 m.
Thus the Reynolds number simplifies to:
Re = (.45 x vmph x 1.5) / (15 x 10-6) = 4.5 vmph
or at stall speed of 50 mph: Re = 1.8 x 106 (you know that 106 = 1,000,000 = 1 million).
Keep in mind the above values are for a 5 ft. chord. For a 2-1/2 ft. chord typical of tail surfaces or the tip of a tapered wing, the Re will be only 1/2 above values.
If the air is looked at, not as a continuous medium, but composed of small balls (the molecules of modern physics), there is obviously an average distance between those balls. The Reynolds number is then nothing else than the relation between the typical solid body length to this average distance between the molecules of the air in which the solid is moving.
As long as this Reynolds number is between the values of .4 x 106 (400,000) and some 10 X 106 (ten million) what we will say about airfoils will apply.
Note that for smaller Re (say 10,000 to 400,000, which is the range for radio controlled models and smaller windmills), other lows apply; however, we will not consider these numbers in this present set of articles which deal with light planes. The same applies at very large Reynolds numbers, which are practically associated with Mach numbers larger than .3, where the compressibility of the air can no longer be neglected as it is in classic aerodynamics which considers the air as an incompressible, continuous medium.
Boundary Layer
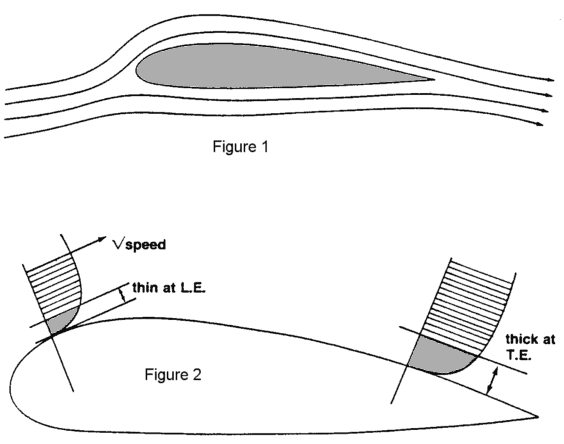
When the air hits the airfoil leading edge it will separate into the upper and lower airstream, which meets again at the trailing edge. (See Figure 1).
It is obvious that the air very close to the airfoil "rubs" against the solid surface and is slowed down. In other words, starting downstream of the impact point, the air loses some of its momentum, or velocity. And it loses more and more as we follow it along the path close to the solid airfoil. We can see that friction creates an area where there is less speed. The reduced speed area just outside of the airfoil becomes thicker and thicker as we follow it from the leading edge to the trailing edge. This area is called the boundary layer. Its thickness is increasing as described and is defined as the thickness at which the local free stream speed is finally reached. A typical boundary layer thickness is 1/2" near the trailing edge. The friction, which obviously, is a loss, results in the friction drag of the airfoil.
Again the theory of fluid dynamics shows that there are two possible types of stable boundary layers:
1. The first, to build up, is called 'laminar" because the flow is nice and steady and the friction drag is relatively low.
2. The second is called 'turbulent" because the flow is rather rough and the friction drag is higher.
The unfortunate thing is that the "laminar boundary layer" will automatically become turbulent (with associated higher drag) close to the leading edge of the airfoil unless very special precautions are taken. These precautions are:
1. A very smooth airfoil surface: Slight construction defects (or bugs as they stick to the airfoil leading edge) will change the laminar boundary layer into a turbulent one. Unless you have a perfect airfoil and keep it this way forget about the gain possible with a laminar flow!
2. A special shape of the airfoil: The pressure distribution on the airfoil is related to the airfoil shape. Today we can calculate (with high speed computers) airfoils which maximize the length of the laminar boundary layer. Still, what is mentioned in a) applies. But, do not get desperate. The friction drag of the airfoil with a laminar boundary layer is .08, whereas in turbulent flow it becomes .12. Sure, this is a 50% increase but only on the friction drag of the airfoil. The other drag contributions are airfoil shape, wind induced drag, tail drag, fuselage and landing gear drag, interference drag, cooling drag and a few more. Your aircraft will never go 50% faster just by changing the airfoil - at the very best, you may gain a few (3 to 5) percentage points.
Airfoil Design and Geometry
I will simply refer you to a very good (and understandable) book, Theory of Wing Sections by Ira Abbott and Albert Von Doenhoff (Dover, 1959), available as a reprint from EAA. Get your copy and study it a bit. In our next article we will go on with our consideration of airfoils.